
In 3D space, the star can go in any combination of three directions.
So, we will need the shifts for the X, Y and
Z values.
We can also throw in the Annual Shift for the SGC T coordinate,
which is actually going to be just the change of distance the star makes
from our Sun in a year. Now, armed with these numbers, it will be much
easier to do, otherwise tough, navigational problems. Why? Because, working
with a coordinate system is much easier, math wise, than working with trajectories.

Stars are in a state of movement relative to the SGC zero coordinate (our Solar System's barycenter) and will therefore constantly shift their SGC coordinate values. The change of position of a star relative to our Solar System is dependent on many factors. To arrive at a prediction of an Annual Shift in the SGC system, the star in question can be precisely observed for movement. In general terms, these aberrations are already known values and are defined as being either planetary aberration; motion of the star (emitter), or stellar aberration; motion of the observer. Such movements and aberrations are:
5.1.1
| Annual Shifts of a star in SGC Coordinates | ||||
|---|---|---|---|---|
| Source | Data In | Data Out | ||
| Tri-Coordinate formulae 2.3.8, 2.3.9, 2.3.10 | The apparent SGC coordinates of X,Y,Z for a star and T. |
|
||
| known | Apparent Stellar Distance to a star (ASD), based on the star's apparent position as seen from Earth. ASD is not adjusted for the movement of the star after light, we currently can see from Earth, has left the star. | Real Stellar Distance to a star (RSD), adjusted
to place the star in it's current true position, relative to itself, although
this position cannot be seen from Earth.
|
||
| Tri-Coordinate formula 2.2.1 | Galactic declination of a star (Gd) |
|
||
| Tri-Coordinate formula 2.2.2 | Galactic Right Ascension of a star (Gr) |
|
||
| known | Proper Motion of a star (u) in degrees / per year of an arc of a great circle created by the observed movement of the star. | |||
| known | Radial velocity of a star (RV) in kilometers / sec. Stellar movement toward or away from 0,0,0, calculated by various accepted methods such as parallax shift over long periods of observation or the red shift of the starlight. | |||
| Galactic Proper Motion formulae 4.1.7 | The galactic polar angle of Proper Motion of a star (G ) ) |
|||
| Measured | All other aberrations that affect the star's movement. | Overall Error of Measurement due to limits of measure. (OEM) | ||
| All above Data In values used to find this data... | Annual Shift of movement of a star given as positive or minus values; (XAS, YAS, ZAS, TAS) | |||
The above list, I admit, is confusing. All that is done here is to make
a complete list of all possible values regarding stellar movement.
It is interesting that the obvious value of the actual speed of the star's Proper Motion is not in the above list. This is not needed, because once the SGC Annual Shift values are found, this value will automatically become part of the SGC measurement.The following graph can perhaps help to understand why so many values are important.
Graph 5.1.2
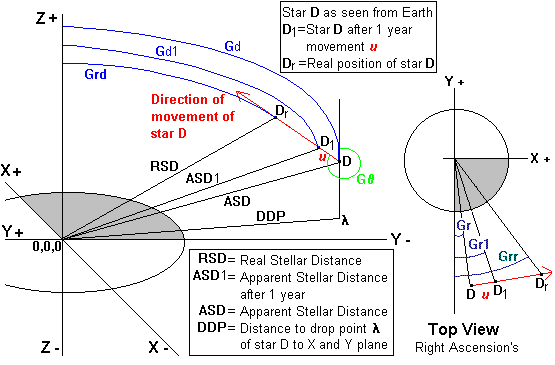
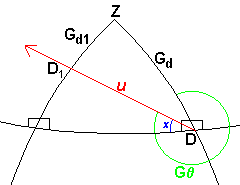
Refer to the above table for all the definitions of the Gd and Gr terms. The main thing to notice here is why each one has a different value.
Two points to consider:
1) The star D moves to it's new position D1 after one year, but in reality when the observer on Earth sees star D it is really at Dr because it has moved that far in the time it takes for the light to travel from star D to Earth.2) An interesting advantage of the SGC system is that in spite of the fact that the Earth and the Sun are moving as well along the X axis, this movement does not need to be shown or considered because the accurately plotted movement of star D along the red line includes any such variations. This allows for solutions to always use 0,0,0 as a middle point even when finding stellar positions such as D, or D1, a year later, or even Dr a stellar position that is at a point several years along the line of movement. This is a important feature because it removes any extraneous computations that would be caused by a moving Earth coordinate. Any designation of a change of position of Earth due to a movement along the X axis, needs only to be referred to by a change in it's T coordinate (see 3.0).
The SGC system is not a shortcut to this measurement process, but it can make results more easily useable because the Annual Shifts may be plotted in SGC coordinates. Such a comprehensive chart can be an aid to the study of the overall movements of star groups and help to visualize the three dimensional positions of stars. The chart could also quickly give the user an idea of distances between any two stars. The SGC system can use such a list of coordinates to describe the movements of each star, similar in nature to the rise and set time star lists which assist in nautical navigation.
Since the SGC incorporates aberrations and main stellar
movements within the Annual Shift values, once these Annual Shifts are
computed and listed, further reference to aberrations and movement may
be ignored while comparing stellar positions within the SGC system.
Furthermore, the aberrations caused by our Solar System wobble or by the
Earth's movement around the Sun or even by the wobble caused by the moon
gravitational pull can also all be ignored for computations and plotting
within the SGC system. What is valid to the SGC system is
the change of distance and the direction of movement a star compared to
our Sun (or more accurately our Solar System's barycenter). The fact that
it is impossible to accurately measure this from our moving Earth, without
factoring out the wobble type of aberrations is a problem for the earthbound
astronomer.
Point of interest: An earthbound astronomer is faced with calculating out many aberrations to find the real stellar movement. Astronomical constants for changes in our Solar System's direction of movement standardized to the epoch Julian year 2000, show changes of our direction of movement through the galaxy caused by our galactic orbit. These changes for our Solar System are:These aberrations are, in other words, the Solar System's wobble and arc as it orbits the Milky Way galaxy.
- The annual precession in Right Ascension is 3.0749575 seconds.
- The annual precession in declination is 20.043109 seconds.
- The annual constant of nutation is 9.2025 seconds (the inclination of the solar axis to the vertical).
- The annual constant of aberration is 20.49552 seconds (the inclination of the solar axis to the direction of movement).
This slowly changing arc of the Sun's galactic orbit will have an effect, however minute, on observed distances and movements of other stars. More on this in Chapter 7.0. The SGC system sidesteps this issue by creating the Annual Shifts. If the Annual Shifts are kept accurate and current, they will automatically include any changes caused by our Sun's galactic orbit.
First, let us look only at the movement across the sky, disregarding,
for the moment, any changes in distance. To find a new galactic Right Ascension
and galactic declination after one year of stellar motion one must have
the following data:

The table below shows how the stellar movement may
be resolved in values of galactic Right Ascension and galactic declination.
All possible solutions for each value of G are given. The graphs show the declination solutions where the star D
travels to D1 in one year along the arc of Proper Motion
u. (The angle x is added for reference as an
angle needed to complete the computations but it is not directly referred
to in the formulae below.)
are given. The graphs show the declination solutions where the star D
travels to D1 in one year along the arc of Proper Motion
u. (The angle x is added for reference as an
angle needed to complete the computations but it is not directly referred
to in the formulae below.)
5.1.3
Galactic Right Ascension (Gr1) and galactic declination (Gd1) change after one year |
|
When G is: is: |
Formulae to find galactic Right Acension and galactic declination after one year. |
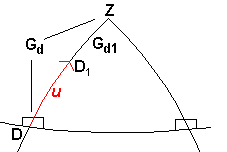
G  = 0° = 0° |
Gr1 = Gr
Gd1 = Gd - u |
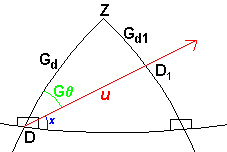
0° < G  > 90 ° > 90 ° |
Gr1 = Gr + [u (cos (90
° - G ))] ))]
Gd1 = Gd - [u (sin (90° - G  ))] ))] |
G  = 90° = 90° |
Gr1 = Gr + u
Gd1 = Gd |
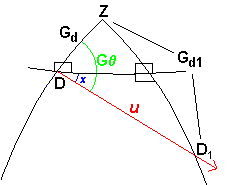
90° < G  > 180 ° > 180 ° |
Gr1 = Gr1 + [u (sin (180
° - G ))] ))]
Gd1 = Gd + [u (cos (180° - G  ))] ))] |
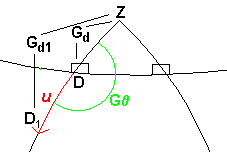
G  = 180° = 180° |
Gr1 = Gr
Gd1 = Gd + u |
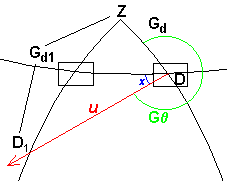
180° < G  > 270 ° > 270 ° |
Gr1 = Gr - [u (cos (270
° - G ))] ))]
Gd1 = Gd + [u (sin (270° - G  ))] ))] |
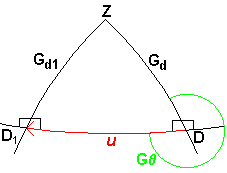
G  = 270° = 270° |
Gr1 = Gr - u
Gd1 = Gd |
270° < G  > 360° > 360° |
Gr1 = Gr - [u (sin (360
° - G ))] ))]
Gd1 = Gd - [u (cos (360° - G  ))] ))] |
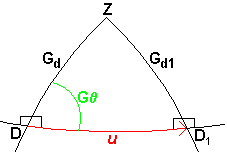
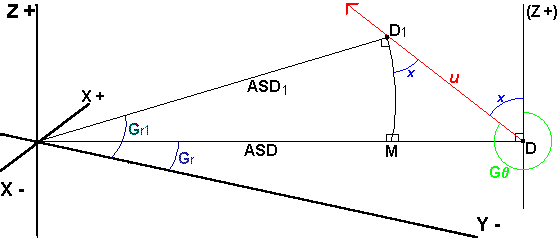
Let's have a closer look at one of the solutions for
Gr1.
Graph 5.1.4. below shows the angles and points
required to find the new galactic Right Ascension, (Gr1)
of star D as it moves to point D1 after one year
of Proper Motion u. In this example G = 300 ° and therefore the formula to use is at the bottom of the chart
5.1.3 above.
= 300 ° and therefore the formula to use is at the bottom of the chart
5.1.3 above.
Graph 5.1.4
Where Gr = the current galactic Right Ascension and
Gd= the current galactic declination and where Gr1
= galactic Right Ascension of the star after one Earth year, and Gd1
= galactic declination of the star after one Earth year and u
= Proper Motion (the actual speed of the star's movement in degrees), G = angle of Proper Motion based on galactic polar (see 4.0).
= angle of Proper Motion based on galactic polar (see 4.0).
The problem then is to find Gr1 when given is;
Gr, ASD, ASD1, u and
G .
(Note that the right angles are true but look a little off because of the
problem of trying to show three dimensions on a two dimensional illustration.)
Angle x is the angle shown in the formula listed below as
(360 ° - G
.
(Note that the right angles are true but look a little off because of the
problem of trying to show three dimensions on a two dimensional illustration.)
Angle x is the angle shown in the formula listed below as
(360 ° - G ). Once angle x
is found it can be shown to be part of triangle DD1M. This
is true because the angle MDD1 + angle x
= 90 ° and DMD1 is a right angle. This allows the angle
x at location DD1M to be used in the formula
to find the segment
D1M. Finally subtracting D1M
from
Gr will give the sought value of Gr1.
). Once angle x
is found it can be shown to be part of triangle DD1M. This
is true because the angle MDD1 + angle x
= 90 ° and DMD1 is a right angle. This allows the angle
x at location DD1M to be used in the formula
to find the segment
D1M. Finally subtracting D1M
from
Gr will give the sought value of Gr1.
5.2.1
Where ASD1 = the distance to the star after one year of movement, RV = radial velocity km /sec (positive or negative), J = seconds in a year (31,557,600), and ASD = the distance of the star at the beginning of the year. (Just as ASD = the T coordinate, ASD1 is equal to T1, the new time coordinate of the star after one year.)
With this new stellar postional data; firstly, from the table of formulae 5.1.3 showing the new galactic angles and secondly, the above formula 5.2.1 showing the distance of a star after one year of movement, we now have all the data we need to find the new SGC coordinates of the star after one year of movement. Using the new data for Gr1, Gd1 and ASD1, the formulae 2.3.7 through 2.3.10 may now be run again to give us four new coordinates which we will call X1, Y1, Z1 and T1.
The difference between X1, Y1,
Z1
and T1 and the current X, Y,
Z
and T coordinates will give us the Annual Shifts XAS, YAS,
ZAS
measured in a fraction of a light year and TAS measured in time.
5.2.2
Y1 - Y = YAS
Z1 - Z = ZAS
ASD1 - ASD = TAS
Note the TAS represents the shift in the SGC T coordinate due to the change of distance of the star compared to the Sun. Remember that the SGC T coordinate becomes greater the further the star is away from the Sun. (see 3.0)
Finding the Real Position Values would otherwise be
a quite difficult math problem, but is much easier because all the values
are now within the SGC system. The Real position Values are derived
by simply multiplying the SGC T value (the apparent light year distance
to the star) to each ?AS value and adding the sum to the SGC
coordinates X, Y, Z and T.
5.3.1
(T YAS) + Y = Yr
(T ZAS) + Z = Zr
(T TAS) + T = Tr = RSD
The final values to find are the the Real galactic
Right Ascension, Grr and the Real galactic declination, Grd.
These are the values that would allow you to know exactly which direction
to aim a starship for the current position of a star and allow you to resolve
such problems as to which direction to aim a starship to redezvous with
a star in x number of years.
5.3.2
One may multiply the Proper Motion, u, by the RSD
to find a new
u1 value which reflects the Real Stellar
Distance. Use this
u1 value instead of u
and preform the calculations in the table 5.1.3
again. The results will give the Grr and Grd values in place
of Gr1 and Gd1.
Return to Table of Contents | The Appendix Last updated: October 3, 2002 |