

4.0.1
| Galactic Proper Motion | ||||
|---|---|---|---|---|
| Source | Data In | Data Out | ||
| known | 1) The Earth polar declination of the star (d) | |||
| known | 2) The Earth polar declination of the galactic north (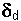 ) ) |
|||
| known | 3) The Earth polar angle of Right Ascension of the galactic
north (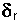 ) ) |
|||
| known | 4) Stellar angle of Proper Motion based on Earth polar
( ) ) |
Stellar angle of Proper Motion based on galactic polar
(G ) ) |
||
GIllustration 4.0.2
 may be found from the above values. The
G
may be found from the above values. The
G differs from the
differs from the  ,
because the Earth pole and galactic pole point to different zeniths and
therefore any angle relating to one pole will almost always be a different
angle relative to the other pole. Since we are dealing with a simple directional
angle between 0° and 360°, we shall only need only to add or subtract
an angle to change from Earth polar to galactic polar. However, the amount
of the angle adjustment will vary, depending on where the star is in the
sky.
,
because the Earth pole and galactic pole point to different zeniths and
therefore any angle relating to one pole will almost always be a different
angle relative to the other pole. Since we are dealing with a simple directional
angle between 0° and 360°, we shall only need only to add or subtract
an angle to change from Earth polar to galactic polar. However, the amount
of the angle adjustment will vary, depending on where the star is in the
sky.
Graph 4.0.3

Where stars A, B, and C show sample stellar positions
looking up from the Earth at both the Earth polar zenith, N, and
the galactic polar zenith, Z. The red arrows indicate the direction
of the star's movement or "direction of Proper Motion" shown by the small
red letters, a, b and c. This
angle of this direction is defined by drawing a line from the star to the
North Pole, N and taking the angle clockwise around to the red line,
the direction of the star's movement. This is shown on the graph as the
small black arcs around each star and is a known value of the star commonly
called the "angle of Proper Motion". For this paper it will be further
clarified as the "Stellar angle of Proper Motion based on Earth polar"
and designated as  .
.
My purpose here is to find the "Stellar angle of Proper Motion
based on galactic polar" shown on the graph in green as G .
The blue arc's shown as the three angle's v, one for each
sample star, show the angle between the Earth pole N and the galactic
pole Z as subended by the star. The value of v is
the one which we seek in order to preform the transfer of
.
The blue arc's shown as the three angle's v, one for each
sample star, show the angle between the Earth pole N and the galactic
pole Z as subended by the star. The value of v is
the one which we seek in order to preform the transfer of  to G
to G . The arc
. The arc 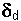 is
the declination of the galactic polar and is a known value.
is
the declination of the galactic polar and is a known value.
Note how the G values for each star
compared to the
values for each star
compared to the  values. For stars A
and C, G
values. For stars A
and C, G is larger than
is larger than  ,
but is smaller for star B. Also note that star's B and C's
red arrow, direction of Proper Motion is aimed between the Earth pole,
N and the galatic pole
Z. On close inspection, it can be
seen that the amount of change in such angles is clearly dependent on the
star's position relative to the galactic north and it's direction of Proper
Motion.
,
but is smaller for star B. Also note that star's B and C's
red arrow, direction of Proper Motion is aimed between the Earth pole,
N and the galatic pole
Z. On close inspection, it can be
seen that the amount of change in such angles is clearly dependent on the
star's position relative to the galactic north and it's direction of Proper
Motion.

4.1.1 (known) NZ =The cosine of angle v may be stated using a standard trigometric formula as:= declination of the galactic polar (known) NA = declination of star A (known from formula 2.2.1) ZA = galactic declination of star A (Gd) G
= angle v +
4.1.2

Once angle v is found, the only question is whether to
add it or subtract it from  . In the example
star A, simple addition will work. But this will not work for either
of the other stars. The formulae we seek needs to be more refined.
. In the example
star A, simple addition will work. But this will not work for either
of the other stars. The formulae we seek needs to be more refined.
The examples in graph 4.0.2 show that stars
A and B are in the hemisphere defined as the Earth pole N
lies to the right of the galactic pole Z. Any stars in this so defined
hemisphere require an addition of the angle and angle v to find G
and angle v to find G .
.
+ v = G
4.1.3
(With the example star B, the simple addition will work, if one keeps in mind that any amount of degrees over 360, a full circle, results in a number x° which can also be accurately defined as x° - 360°.)Star C is in the hemisphere where N is to the left of Z and a subtraction is required;
If one examines the situation of star C closely, it can be seen that- v = G
4.1.4
 is about 20°, while G
is about 20°, while G would be about 310°. But trying to get this answer from formula 4.1.4
is not possible. The
angle v for star C (angle
NCZ) can be found using formula 4.1.2. Let us say it is 70°.
Substituting values for formula 4.1.4 gives us:
would be about 310°. But trying to get this answer from formula 4.1.4
is not possible. The
angle v for star C (angle
NCZ) can be found using formula 4.1.2. Let us say it is 70°.
Substituting values for formula 4.1.4 gives us:
20° - 70° = -50° 4.1.5Clearly we need even more refined formulae that takes all the possibilities into consideration. Where it is understood, as with example star B, if one goes totally around the circle, i.e. greater than 360° the true value of the angle is never greater than 360°. By the same token, if the degree value is less than zero, as in the case of star C, the true angle may be restated as a positive value:
360 ° + -50° = 310° 4.1.6The set of formulae to find the angle of Proper Motion based on galactic polar, G
 can be stated as:
can be stated as:
4.1.7
Solutions to G |
||||
|---|---|---|---|---|
| (Hemisphere)
Position of Star based on given RA |
For this value | Do this formula | ||
| (N to the right of Z)
( 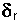 - 180°) < RA < - 180°) < RA < 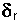 |
 + v < 360° + v < 360° |
G = =  + v
+ v |
||
 + v = 360° + v = 360° |
G = v = v |
|||
 + v > 360° + v > 360° |
G = 360° - ( = 360° - ( + v)
+ v) |
|||
(N to the left of Z)
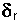 > RA > ( > RA > (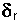 -180°) -180°) |
 - v < 0° - v < 0° |
G = 360° - ( = 360° - ( - v)
- v) |
||
 - v = 0° - v = 0° |
G = v = v |
|||
 - v > 0° - v > 0° |
G = =  + v
+ v |
|||
(The star is on the circle described by N and Z)
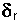 = RA, or RA = ( = RA, or RA = (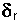 -180°) -180°) |
G = 0° = 0° |
|||
Where RA = Earth polar Right Ascension of the star, 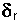 = the Earth polar angle of Right Ascension of the galactic north pole (a
known value), v = the angle subended by the star and N
and Z,
= the Earth polar angle of Right Ascension of the galactic north pole (a
known value), v = the angle subended by the star and N
and Z,  = Stellar angle of Proper Motion
based on Earth polar.
= Stellar angle of Proper Motion
based on Earth polar.
Return to Table of Contents | The Appendix Last updated: October 3, 2002 |