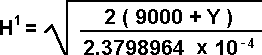7.0 Estimated Deviations
This chapter just covers the loose-end details regarding deviations, a
topic that astronomers love to discuss. I show how there may be some minor
deviations in stellar Annual Shifts caused by galactic orbit of the Sun
compared to other star's galactic orbits and then I point out that these
changes are very small. They can easily be handled by a complete SGC
database of Annual Shifts. I also show that much of the minute deviations
are actually much less than the accuracy of our current measurments, so,
at the moment, they are a mute point.

This is a more detailed summary of the estimated deviations and aberrations
and how they apply to the
SGC system. The deviations presented here
are not planetary or emitter aberiations presented in
5.0.
Rather they are to do with the larger scale of the galactic orbit of stars
and other errors of measurments due to technical limitations. At present
most all of the deviations in this chapter are beyond our present ability
to measure.
7.1 Proper Motion and Radial Velocity
Stars travel in a curved galactic orbit. The Radial Velocity and Proper
Motion of a star are based on the concept that the star travels in a straight
line. The difference between the straight line course and the curved galactic
orbit will be very minimal for time spans less than 10,000 years. In fact
the overall limits of accuracy will make any compensations meaningless
until a more accurate measurement system of the future.
Formulae may be used to find such deviations as long as one assumes
the stars are following basically circular orbits around the galactic center.
(This is not the case because of other stellar gravitational fields, friction
from stellar dust, etc.) The assumption of a circular galactic orbit will
be used to show a general case.
To make matters worse, deviations will appear to be different
as viewed from our moving solar system. If the star is closer to the galactic
center, it will appear to be orbiting faster then our Sun and it will appear
to approach us, reach a nearest point, and then move away. If the star
is further away from the galactic center, it will appear to be moving more
slowly than us. We will appear to catch up with it, reach a nearest point
and then depart from it.
To make some sense of the different possibilities as viewed from
our solar system, one must consider:
-
In what sector the star lies.
-
The distance to the star.
-
It's galactic angle of Proper Motion.
The following chart highlights the problem of apparent motion and how it
is observed from our moving Solar System. It shows eight sectors of space
defined by the X, Y and Z axis. The changes in apparent
Proper Motion, Radial Velocity and Galactic angle of Proper Motion are
shown. For this example, the chart only shows stars which are rotating
around the galaxy in an X positive and Y negative direction.
7.1.1
Apparent Motion of stars as viewed from our Solar System at 0,0,0 over
extreamly long observation
|
| Sectors |
Spinward or counter-spinward / coreward or rimward
from 0,0,0 |
Proper Motion |
Radial Velocity
+ towards 0,0,0
- recedes from 0,0,0 |
Galactic angle of Proper Motion
G |
| alpha & kappa |
X+ Y+ Z+ or Z -
(spinward / rimward) |
slows |
+ towards 0,0,0 |
180° - 360° * |
| beta & sigma |
X - Y+ Z+ or Z -
(counter-spinward / rimward) |
quickens |
- recedes from 0,0,0 |
180° - 360° * |
| gamma & tau |
X - Y - Z+ or Z -
(counter-spinward / coreward) |
quickens |
+ towards 0,0,0 |
180° - 360° * |
| delta & omega |
X+ Y - Z+ or Z -
(spinward / coreward) |
slows |
- recedes from 0,0,0 |
180° - 360° * |
* It seems an apparent unlikely situation to show the galactic
angle of Proper Motion in the above chart to be limited to only 180°
- 360°. It must be remembered, that the assumptions made in section
7.1 above limits the direction of galactic orbit and therefore makes the
stars appear to be moving in one general direction.
7.2 Special cases
-
In the case of a star lying exactly on the Y axis i.e with a zero
X value, the Proper Motion will have reached it's peak and the Radial
Motion will be at zero.
-
In the case of a star lying exactly on the X axis, the star would
still belong to the nearest spinward sector.
-
In the case of a star lying in a Y negative area very close to the
X axis. This star may act as if it belonged to the adjacent spinward
sector because it's galactic orbit could lie outside the Sun's orbit.
-
In the case of a star lying in a Y negative area close to the X
axis and with a zero
Z value. This star, if lying exactly on the
same orbital path as the Sun, will not change it's Proper Motion and the
Radial Velocity would be zero.
7.3 The problem of the validity of any measurements for deviation in the
galactic orbit
The Sun moves at from 220 km/sec to 250 km/sec towards the Cygnus constellation
(spinward along the
X positive axis). This is generally called the
Solar Galactic Movement (SGM). Assuming an estimated velocity of
235 km/sec and a circular galactic orbit with a estimated radius of 9000
parsecs, the revolution once around the galaxy, based on these numbers,
would take 235,321,864 years.
Galactic stellar orbits have, as mentioned above, different speeds
(differential rotation). These speeds can be estimated, however, there
are some problems in resolving this.
-
The center bulge of the galaxy causes a deviation from a true Kepler's
third law of planetary motion.
-
Local gravitational effects of star groups, random collisions and even
Z elevation orbits of Population II stars can affect a galactic orbit.
(Population II stars rotate around the galaxy with inclined orbits that
take them above the galactic plane.)
So, absolute values of orbital speeds and deviations of stars will be extremely
difficult, if not impossible to predict.
7.4 Using the SGC system to find a galactic orbit
One interesting point where information can be drawn directly from the
SGC system coordinates is a follows: One could use the distance
to the galactic center to find the orbital velocity of any star (assuming
a perfect circular orbit). Also assuming that the Sun is 9000 parsecs to
the galactic center, it is a simple matter of using the Y coordinate
value to find the star's distance to the galactic center and therefore
it's approximate galactic orbital speed.
7.4.1
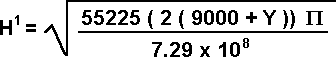
Based on the simple geometric rule,  D
= C. Where
H1 is the estimated galactic orbital
speed of the star at coordinate Y. The value 55,225 is the estimated
Sun's velocity (235 k/sec squared) and the 7.29 x 108 represents the galactic
radius of the Sun to the galactic center of 9000 parsecs. This can be reduced
to:
D
= C. Where
H1 is the estimated galactic orbital
speed of the star at coordinate Y. The value 55,225 is the estimated
Sun's velocity (235 k/sec squared) and the 7.29 x 108 represents the galactic
radius of the Sun to the galactic center of 9000 parsecs. This can be reduced
to:
7.4.2
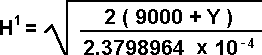
It would also be possible to figure the postional deviations of stellar
orbits using spherical trigonometry and Kepler's third law of planetary
motion. This solution requires some extensive math. As previously stated,
the end result would have no validity because of the inaccuracies in current
measurements and other deviations. So I will end this section here.
7.5 Overall Error of Measurement
A more useful measurement is an Overall Error of Measurement (OEM).
This can show the limits of accuracy and thereby give a overall limit to
resolution or accuracy of the entire SGC system. By far, the weakest
link, to date, is the current levels of accuracy for stellar distances.
The OEM can be found as follows:
For less than 15 light years = ± 0.1% error.
For greater than 15 light years = ± 3% error.
For greater than 100 light years, star distances are otherwise rounded
to 2 significant digits.
371 is changed to 370, 2771 is changed to 2800.
Backward to Chapter 6 - Using the SGC system to resolve
problems in navigation
Return to Table of Contents |
The
Appendix
Last updated: October 3, 2002 |



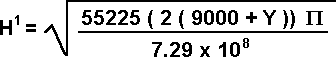
 D
= C. Where
H1 is the estimated galactic orbital
speed of the star at coordinate Y. The value 55,225 is the estimated
Sun's velocity (235 k/sec squared) and the 7.29 x 108 represents the galactic
radius of the Sun to the galactic center of 9000 parsecs. This can be reduced
to:
D
= C. Where
H1 is the estimated galactic orbital
speed of the star at coordinate Y. The value 55,225 is the estimated
Sun's velocity (235 k/sec squared) and the 7.29 x 108 represents the galactic
radius of the Sun to the galactic center of 9000 parsecs. This can be reduced
to: