6.0 Defining SGC measurement values for coordinates and course heading

In overview:

• Values relating to Apparent Coordinate Positions as viewed from Earth or any mid-mission point.
• Values relating to the Real Stellar Position which cannot be viewed directly when the light arriving is multiple years old.

The course directional values are either:

• Earth Polar based - which keep the traditional values of Right Ascension 0 to 23' 59.999..." and declination 90º to -90º (Polaris to Southern Cross).
• Galactic Polar based - which adopts a new number format replacing Right Ascension with 0 to < 4 and declination with 1 to -1.  No degrees are used and the method of declaring course headings has specfic rules.  For example; all Galactic Polar based course headings are preceded with G for galactic. Hopefully, this will keep everyone from accidentally mixing up of Galactic Polar based course values with Earth Polar based values, a mistake which could cause disaster.

1. Celeste, our navigator, needs to take a sighting on a star in mid-mission. She can use the SGC system to more accurately locate the apparent position of the star.

 
2. Taking a sighting on the destination star, Sirius, Celeste can make use of it's Annual Shift to predict at what X, Y, Z and T coordinate Sirius will be at the Nearest Point of Intersection, (NPI), of her ship and Sirius based on her speed of travel.

 
3. The SGC System can show the stars charted with their Real Stellar Distance, (RSD), or in their Apparent Stellar Distance, (ASD), as viewed from any location.

1. Celeste may sight back at the Earth from a mid-mission point and find the Real Stellar Distance (RSD) of the Earth. She may also find the position of where the Earth will be in order to receive a speed of light radio transmission or where it will be to rendezvous with on a return trip.

 
2. The SGC system can also assist Celeste in stellar triangulation. Stars appear to be in a different position depending on from where they are viewed. Stars chosen for triangulation should ideally be as near as possible. This will increase their parallax shifts and enable Celeste to make a more accurate positional computation.

Note: Chapter 6 helps define many, but not all, possible SGC navigation problems. Further examples could be made into a SGC navigational reference. I will now only attempt to lay the groundwork in understanding and resolving SGC navigational problems.

 For interstellar flights of say, less than 20 light years, it would seem that a direct sighting of the destination star and some backup triangulation would be sufficient. However, as interstellar trips become longer and more complex, it will be useful to be able to factor out such inherent errors in the Apparent Stellar Distance, ASD, of the triangulation stars as viewed from Earth compared to their positions as viewed from a starship in mid-mission.

6.1 Finding real and apparent distances from SGC values

 Since we are dealing with a multitude of confusing points and apparent distances, it would be wise at this time, to go over some Point Abbreviations comparing points and distances as seen from 0,0,0 versus as seen from a mid-mission point M:
 
 

                                                    6.1.1

Let us return to the example of our navigator, Celeste, and her mission to Sirius. Before she embarks on the Sirius mission she could easily resolve some navigational problems of distance. With her complete SGC chart and list of Annual Shifts, she would know the real coordinates of Sirius as well as the apparent coordinates. Knowing, also, that her average planned velocity for the mission is .36c, it becomes a simple matter to find the real distance to Sirius using the good ole pythagorithian right angle hypotenuse rule in 3D.
 
 

                                                    6.1.2

Where Xr, Yr, Zr are the real coordinates for Sirius, S'RSD'm is the Real Stellar Distance from 0,0,0.

Using this RSD distance, Celeste may also easily find the time t in Earth years, it would take to travel this far based on her average velocity of travel, AVT, of .36c (.36 the speed of light).
 
 

                                                    6.1.3

Unfortunately, it is not as easy as that to resolve a distance required to travel to a moving star, because one must consider that the star is moving towards or away from 0,0,0. Simply knowing how far it is at any given time, will not tell you how far the ship will need to travel to meet the star. The point of rendezvous of a starship with the star will be called NPI the Nearest Point of Intersection. (This issue will be resolved later in an example in 6.5 below.)

Let's look closer at a particular mission in order to understand the navigational problems regarding distance. Suppose Celeste is now almost half way into the mission, 4 light years from Earth but still 5 light years from Sirius. How can one find the remaining real distance to Sirius from a mid-mission point? It is easily done using SGC with only a one line formula!
 
 

                                                    6.1.4

Where Xr, Yr and Zr are the real coordinates of Sirius, a known value, and X'm, Y'm and Z'm are the ship's X, Y and Z coordinates, a measured value. RSD is then the real distance from the ship at mid-mission point M to Sirius.
 
 

Note: This formula turns out to particularly important if Celeste has strayed from a direct course. This would result in a situation where she may be 4 light years from Earth but more than 5 light years from Sirius. In that case, formula 6.1.4 would set the record straight and allow for accurate calculations to be made.

However, if Celeste wishes to do a visual sighting for Sirius, she must work with the ASD, Apparent Stellar Distance to Sirius and not it's RSD, Real Stellar Distance. (She would obviously also need to know the ASP Apparent Stellar Position as seen from her ship, i.e. Sirius's apparent galactic declination and galactic Right Ascension. This question is covered in 6.2. Section 6.1 is only about distances, let's stay for now, with only the distance question.)

 The light arriving from Sirius is as old as how many light years Celeste is away from Sirius. When we check the above table 6.1.1, we find that this distance is referred to as S'ASD'm. So, for Celeste to find how far away Sirius appears to be, she must know this value.

                                                    Graph 6.1.5

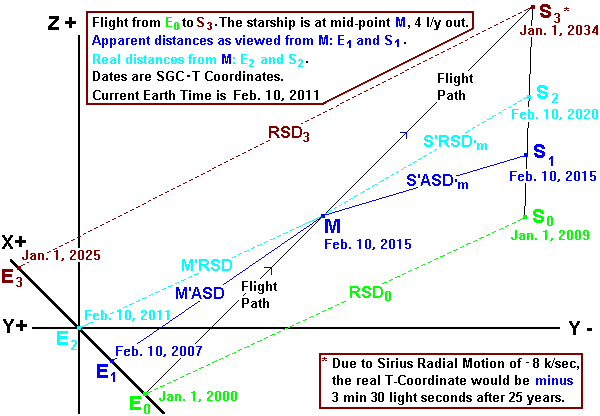
Where the current Earth time is Feb. 10, 2011. The mission route is shown as a solid black line from E0 to S3. The starship is currently at point M. RSD values, the real distances, are shown as dotted lines; the RSD0 from 0,0,0 at E0 to Sirius at S0 at the beginning of the mission is 9 light years. The RSD3 value from E3 to S3 at the end of the mission is 9 light years plus or minus a distance caused by Sirius's Radial Motion. (In reality there would only be a minus 3 minutes 30 light seconds over the 25 year mission.) The ASD, light seen from point M, are shown as solid dark blue lines. At point M, light arriving from the 0,0,0 is 4 years old and from Sirius is 5 years old. All T coordinates are given for each point as dates. (It is a coincidence that the T coordinate for point M and S1 are the same. The 0,0,0, coordinates, our Sun, actually does move slowly towards X +. So, showing the various E coordinates along this line is correct.)

 Celeste started the mission on January 1, 2000 at point E0 and travelling at an AVT (Average Velocity of Travel) of .36c she would reach 4 light years from Earth at point M, on February 10, 2011 CET (Current Earth Time) at point M. When Celeste makes some observations at point M she finds that some odd things have happened.

1. She looks back at Earth and sees it, however, 4 years in the past at it's position of 0,0,0, February 10, 2007, E1. She cannot see it at it's real position at E2, because the light leaving that position has not yet reached her.

 

 
 
 
 
 
 
 
 
 
 
 
 
 

2. She looks at Sirius and sees it at point S1. Celeste is now 4 light years closer to Sirius at point M and therefore Sirius should appear to be about 5 light years away. However, her precise observation of the apparent visible distance to Sirius tells her that it is more than 5 light years away. Why does this happen?

 

 
 
 
 
 
 
 
 
 
 
 
 
 

For this example, let's exaggerate Sirius Radial Motion and say it moves away from Earth and from Celeste at the speed of .01 light year per year.


 

 
 
 
 
 
 
 
 
 
 
 
 
 

Celeste is no longer viewing Sirius where it was at the start of the mission at 0,0,0, 1/1/2000 when it appeared to be exactly 9 light years away. She is now viewing it at the closer distance from point M to S1 or S'ASP'm.

 If Celeste wishes to find the correct distance for S'ASD'm, point M to S1, she could do the following step by step process:

1. The SGC database would give her a Real Stellar Position for Sirius at S2.
2. Celeste could take her own SGC position and find the Real Stellar Distance to Sirius, (S'RSD'm) from point M to S2.
3. Once this distance is known, she can move that amount of time back along the route that Sirius has traveled to find the position of point S1.
4. S1 coordinates compared to her own coordinates at point M would give Celeste the value she seeks; S'ASD'm.

                                                    6.1.6

Where XAS, YAS and ZAS are the known SGC Annual Shifts of Sirius and S'ASD'm is the Apparent Stellar Distance of Sirius as viewed from the ship at point M.

 In fact, even if Celeste had done a little sight seeing and found that she was now 4 light years from Earth but still, say, 7 light years from Sirius, formulae 6.1.4 and 6.1.6 would still work fine because the Real Stellar Distance, RSD, would be greater and this would automatically adjust the solution in formulae 6.1.6.

Note: There is no conflict between the SGC coordinates that Celeste sees of Sirius and the coordinates that her stay at home sister, Candice, sees from Earth as long as Celeste remembers the SGC rule regarding the T coordinate. To arrive at her own mid-mission SGC T coordinate, she must add the distance back to the Earth (at 0,0,0) .

Once this concept is understood, even more complicated distance problems are made easy. It is then possible, for example, to find the Real Stellar Distance between any two stars in the SGC coordinate system. This is just a variation of formula 6.1.4.
 
 

                                                    6.1.7

Where RSD2 represents the distance between a star, P with real coordinates P'Xr, P'Yr, P'Zr and another star, Q, with real coordinates Q'Xr, Q'Yr and Q'Zr.

Going one step further, it is even possible to find the Apparent Stellar Distance as viewed from Celeste's ship at a mid-mission point to a star other than Sirius. The value we seek shall be called ASD4.

                                                    Graph 6.1.8

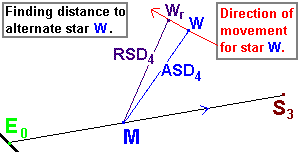
Use a variation of formula 6.1.4 to find the Real Stellar Distance between the starship at mid-mission point M and star W. The Real Stellar Distance between these points shall be called RSD4. Once the RSD4 is found, the coordinates of star W's Apparent Stellar Position relative to the starship at point Mmay be found.
 
 

                                                    6.1.9

Where X'm, Y'm and Z'm are the SGC coordinates of the ship at a point M, RSD4 is the real distance between the starship at point M and star W. W'Xr, W'Yr and W'Zr are star W's real coordinates (given by the SGC star list) while W'X'm, W'Y'm and W'Z'm are the apparent coordinates of star W as viewed from point M.

Using these new apparent positions, W'X'm, W'Y'm and W'Z'm, it is possible to run the last part of formulae 6.1.6 again and get our end goal value for ASD4, the apparent stellar distance from star W to the starship at point M.

                                                    6.1.10

In summary, it can be seen that such a comprehensive SGC chart and list of Annual Shifts can be a great aid to finding interstellar distances, both real and apparent.

6.2 Finding galactic course values from SGC values

1. The galactic Right Ascension
2. Translated to SGC Galactic heading: Gh
3. The galactic declination
4. Translated to SGC Galactic heading: Ga

1. Any point, relative to 0,0,0, (see tables 6.2.1 and 6.2.2)
2. Any point relative to any other point within the SGC system (see formulae 6.2.3)

                                                    6.2.1

                                                    6.2.1.1
Translating Gr to the new SGC value, galactic heading, Gh.

                                                    6.2.2

                                                    6.2.2.1
Translating Gd to the new SGC value galatic altitiude, Ga.

6.3 Rules for SGC Galactic Headings

1. It is too easy to confuse Galactic Right Ascension with Earth Polar Right Ascension and the same with Galactic versus Earth Polar declination.  An error that somewhere down the line may cause headaches and even a disaster.

1. The SGC Galactic headings allow for a shorthand and concise version of galactic courses which will save time and be more easily used for navigational notes, charts, verbal references, etc.

1. Galactic Right Ascension is stated and written as Galactic Header Gh. The values are 0 to < 4.
2. Written abbreviation example is 'Gh1.23', or 'G1.23'
3. If Gh=0, the written abbreviation should be GØ
4. Spoken example is: G 1 dot 2 3
5. If Gh=0, it may be ommited when saying a course or spoken as G null

1. A single vertical line, | , shall divide the written Gh setting from the Ga setting.

1. Galactic declination is stated and written as Galactic Altitude Ga.  The values are 1 to -1.
2. For abbreviation purposes the point is dropped.
3. A Ga value of .567 may be written as an abbreviation '+ 567'
4. A Ga value of -.882 may be written as '-882'.
5. If Ga=0, the written abbreviation should be Ø
6. Spoken examples are: 'plus 5 6 7', 'min 8 2 2', 'planar'
7. If Ga=0, the spoken abbreviation should be 'planar'.

Examples:

• G1.56|-55 - spoken - G 1 dot 5 6 min 5 5
• GØ|62 - spoken - plus 62 or G null plus 62
• G3.66 - spoken - G 3 dot 6 6 planar

Forward to Chapter 7 - Estimated Deviations

Return to Table of Contents | The Appendix

Last updated: October 3, 2002  |